This post complements an earlier discussion of the Pareto distribution in a companion blog (found here). This post gives a side-by-side comparison of the Pareto type I distribution and Pareto type II Lomax distribution. We discuss the calculations of the mathematical properties shown in the comparison. Several of the properties in the comparison indicate that Pareto distributions (both Type I and Type II) are heavy tailed distributions. The properties presented in the comparison (and the thought processes behind them) are a good resource for studying actuarial exams.
The following table gives a side-by-side comparison for Pareto Type I and Pareto Type II.

![\displaystyle \begin{array}{llllllll} \text{ } &\text{.} & \text{ } & \text{ } & \text{ } & \text{ } & \text{ } &\text{ } \\ 8a &\text{Limited} &E[X \wedge d] & \text{ } & \text{ } & \text{ } & \displaystyle \frac{\theta}{\alpha-1} \biggl[1-\biggl(\frac{\theta}{d+\theta} \biggr)^{\alpha-1} \biggr] &\alpha \ne 1 \\ \text{ } & \text{Expectation} & \text{ } \\ \text{ } & \text{ } \\ 8b & \text{Limited} &E[X \wedge d] & \text{ } & \text{ } & \text{ } & \displaystyle -\theta \ \text{ln} \biggl(\frac{\theta}{d+\theta} \biggr) &\alpha = 1 \\ \text{ } & \text{Expectation} & \text{ } \\ \text{ } & \text{ } \\ 8c & \text{Limited} &E[(X \wedge d)^k] & \displaystyle \frac{\alpha \theta^k}{\alpha-k}-\frac{k \theta^\alpha}{(\alpha-k) d^{\alpha-k}} & \alpha>k & \text{ } & \text{See below} &\text{all } k \\ \text{ } & \text{Expectation} & \text{ } \\ \text{ } & \text{ } \\ 9 & \text{VaR} &VaR_p(X) & \displaystyle \frac{\theta}{(1-p)^{1/\alpha}} & \text{ } & \text{ } & \displaystyle \frac{\theta}{(1-p)^{1/\alpha}}-\theta &\text{ } \\ \text{ } & \text{ } \\ 10 &\text{TVaR} &TVaR_p(X) & \displaystyle \frac{\alpha}{\alpha-1} VaR_p(X) & \alpha>1 & \text{ } & \displaystyle \frac{\alpha}{\alpha-1} VaR_p(X)+\frac{\theta}{\alpha-1} &\alpha>1 \\ \text{ } & \text{ } \\ \end{array}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cbegin%7Barray%7D%7Bllllllll%7D+%5Ctext%7B+%7D+%26%5Ctext%7B.%7D+%26+%5Ctext%7B+%7D+%26+%5Ctext%7B+%7D++%26+%5Ctext%7B+%7D++%26+%5Ctext%7B+%7D+%26+%5Ctext%7B+%7D++%26%5Ctext%7B+%7D+%5C%5C+8a+%26%5Ctext%7BLimited%7D+%26E%5BX+%5Cwedge+d%5D+%26+%5Ctext%7B+%7D++%26+%5Ctext%7B+%7D++%26+%5Ctext%7B+%7D+%26+%5Cdisplaystyle+%5Cfrac%7B%5Ctheta%7D%7B%5Calpha-1%7D+%5Cbiggl%5B1-%5Cbiggl%28%5Cfrac%7B%5Ctheta%7D%7Bd%2B%5Ctheta%7D+%5Cbiggr%29%5E%7B%5Calpha-1%7D+%5Cbiggr%5D++%26%5Calpha+%5Cne+1+%5C%5C++%5Ctext%7B+%7D+%26+%5Ctext%7BExpectation%7D+%26+%5Ctext%7B+%7D+%5C%5C++%5Ctext%7B+%7D+%26+%5Ctext%7B+%7D+%5C%5C++++++8b+%26+%5Ctext%7BLimited%7D+%26E%5BX+%5Cwedge+d%5D+%26+%5Ctext%7B+%7D++%26+%5Ctext%7B+%7D++%26+%5Ctext%7B+%7D+%26+%5Cdisplaystyle+-%5Ctheta+%5C+%5Ctext%7Bln%7D+%5Cbiggl%28%5Cfrac%7B%5Ctheta%7D%7Bd%2B%5Ctheta%7D+%5Cbiggr%29++%26%5Calpha+%3D+1+%5C%5C++++++++++%5Ctext%7B+%7D+%26+%5Ctext%7BExpectation%7D+%26+%5Ctext%7B+%7D+%5C%5C++%5Ctext%7B+%7D+%26+%5Ctext%7B+%7D+%5C%5C++++++8c+%26+%5Ctext%7BLimited%7D+%26E%5B%28X+%5Cwedge+d%29%5Ek%5D+%26+%5Cdisplaystyle+%5Cfrac%7B%5Calpha+%5Ctheta%5Ek%7D%7B%5Calpha-k%7D-%5Cfrac%7Bk+%5Ctheta%5E%5Calpha%7D%7B%28%5Calpha-k%29+d%5E%7B%5Calpha-k%7D%7D++%26+%5Calpha%3Ek++%26+%5Ctext%7B+%7D+%26+%5Ctext%7BSee+below%7D++%26%5Ctext%7Ball+%7D+k+%5C%5C+++++++%5Ctext%7B+%7D+%26++++%5Ctext%7BExpectation%7D+%26+%5Ctext%7B+%7D+%5C%5C++++%5Ctext%7B+%7D+%26+%5Ctext%7B+%7D+%5C%5C++++9+%26+%5Ctext%7BVaR%7D+%26VaR_p%28X%29+%26+%5Cdisplaystyle+%5Cfrac%7B%5Ctheta%7D%7B%281-p%29%5E%7B1%2F%5Calpha%7D%7D++%26+%5Ctext%7B+%7D++%26+%5Ctext%7B+%7D+%26+%5Cdisplaystyle+%5Cfrac%7B%5Ctheta%7D%7B%281-p%29%5E%7B1%2F%5Calpha%7D%7D-%5Ctheta++%26%5Ctext%7B+%7D+%5C%5C+++++++++++%5Ctext%7B+%7D+%26+%5Ctext%7B+%7D+%5C%5C++++10+%26%5Ctext%7BTVaR%7D+%26TVaR_p%28X%29+%26+%5Cdisplaystyle+%5Cfrac%7B%5Calpha%7D%7B%5Calpha-1%7D+VaR_p%28X%29++%26+%5Calpha%3E1++%26+%5Ctext%7B+%7D+%26+%5Cdisplaystyle+%5Cfrac%7B%5Calpha%7D%7B%5Calpha-1%7D+VaR_p%28X%29%2B%5Cfrac%7B%5Ctheta%7D%7B%5Calpha-1%7D+++%26%5Calpha%3E1+%5C%5C+++++++++++%5Ctext%7B+%7D+%26+%5Ctext%7B+%7D+%5C%5C++++%5Cend%7Barray%7D&bg=ffffff&fg=333333&s=0&c=20201002)
One item that is not indicated in the table is ![E[(X \wedge d)^k]](https://s0.wp.com/latex.php?latex=E%5B%28X+%5Cwedge+d%29%5Ek%5D&bg=ffffff&fg=333333&s=0&c=20201002) for Pareto Type II, which is given below.
for Pareto Type II, which is given below.
where 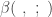 is the incomplete beta function, which is defined as follows:
is the incomplete beta function, which is defined as follows:
for any 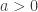 ,
,  and
and  .
.
Discussion
The above table describes two distributions that are called Pareto (Type I and Type II Lomax). Each of them has two parameters –  (shape parameter) and
(shape parameter) and  (scale parameter). The support of Pareto Type I is the interval
(scale parameter). The support of Pareto Type I is the interval 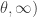 . In other words, Pareto type I distribution can only take on real numbers greater than the scale parameter
. In other words, Pareto type I distribution can only take on real numbers greater than the scale parameter  . On the other hand, the support of Pareto Type II is the interval
. On the other hand, the support of Pareto Type II is the interval 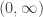 . So a Pareto Type II distribution can take on any positive real numbers.
. So a Pareto Type II distribution can take on any positive real numbers.
The two distributions are mathematically related. Judging from the PDF, it is clear that the PDF of Pareto Type II is the result of shifting Type I PDF to the left by the magnitude of  (the same can be said about the CDF and survival function). More specifically, let
(the same can be said about the CDF and survival function). More specifically, let 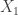 be a random variable that follows a Pareto Type I distribution with parameters
be a random variable that follows a Pareto Type I distribution with parameters  and
and  . Let
. Let 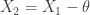 . It is straightforward to verify that
. It is straightforward to verify that 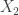 has a Pareto Type II distribution, i.e. its CDF and other distributional quantities are the same as the ones shown in the above table under Pareto Type II. If having the same parameters, the two distributions are essentially the same, in that each one is the result of shifting the other one by the amount
has a Pareto Type II distribution, i.e. its CDF and other distributional quantities are the same as the ones shown in the above table under Pareto Type II. If having the same parameters, the two distributions are essentially the same, in that each one is the result of shifting the other one by the amount  .
.
A further indication that the two types are of the same distributional shape is that the variances are identical. Note that shifting a distribution to the left (or right) by a constant does not change the variance.
Since the two Pareto Types are the same distribution (except for the shifting), they share similar mathematical properties. For example, both distributions are heavy tailed distributions. In other words, they significantly put more probabilities on larger values. This point is discussed in more details below.
Calculation
First, the calculations. The moments are determined by the integral  where
where 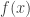 is the PDF of the distribution in question. Because of the PDF for Pareto Type I is easy to work with, almost all the items under Pareto Type I are quite accessible. For example, the item 8c for Pareto Type I is calculated by the following integral.
is the PDF of the distribution in question. Because of the PDF for Pareto Type I is easy to work with, almost all the items under Pareto Type I are quite accessible. For example, the item 8c for Pareto Type I is calculated by the following integral.
In the remaining discussion, the focus is on Pareto Type II calculations.
The Pareto  th moment
th moment  is definition the integral
is definition the integral  where
where 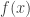 is the Pareto Type II PDF. However, it is difficult to perform this integral. The best way to evaluate the moments in row 5 in the above table is to use the fact that Pareto Type II distribution is a mixture of exponential distributions with gamma mixing weight (see Example 2 here). Thus the moments of Pareto Type II can be obtained by integrating the conditional conditional
is the Pareto Type II PDF. However, it is difficult to perform this integral. The best way to evaluate the moments in row 5 in the above table is to use the fact that Pareto Type II distribution is a mixture of exponential distributions with gamma mixing weight (see Example 2 here). Thus the moments of Pareto Type II can be obtained by integrating the conditional conditional  th moment of the exponential distribution with gamma weight. The following shows the calculation.
th moment of the exponential distribution with gamma weight. The following shows the calculation.
In the above derivation, the conditional 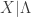 is assumed to have an exponential distribution with mean
is assumed to have an exponential distribution with mean 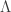 . The random variable
. The random variable 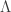 in turns has a gamma distribution with shape parameter
in turns has a gamma distribution with shape parameter  and rate parameter
and rate parameter  . The integrand in the integral in the second to the last step is a gamma density, making the value of the integral 1.0. When
. The integrand in the integral in the second to the last step is a gamma density, making the value of the integral 1.0. When  is an integer,
is an integer,  can be simplified as indicated in row 5.
can be simplified as indicated in row 5.
The next calculation is the mean excess loss. It is the conditional expected value 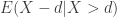 . If
. If  is an insurance loss and
is an insurance loss and  is some kind of threshold (e.g. the deductible in an insurance policy that covers this loss), then
is some kind of threshold (e.g. the deductible in an insurance policy that covers this loss), then 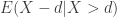 is the expected loss in excess of the threshold
is the expected loss in excess of the threshold  given that the loss exceeds
given that the loss exceeds  . If
. If  is the lifetime of an individual, then
is the lifetime of an individual, then 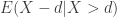 is the expected remaining lifetime given that the individual has survived to age
is the expected remaining lifetime given that the individual has survived to age  .
.
The expected value 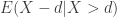 can be calculated by the integral
can be calculated by the integral 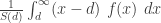 . This integral is not easy to evaluate when
. This integral is not easy to evaluate when 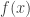 is a Pareto Type II PDF. Fortunately, there is another way to handle this calculation. The key idea is that if
is a Pareto Type II PDF. Fortunately, there is another way to handle this calculation. The key idea is that if  has a Pareto Type II distribution with parameters
has a Pareto Type II distribution with parameters  and
and  (as described in the table), the conditional random variable
(as described in the table), the conditional random variable 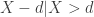 also has a Pareto Type II distribution, this time with parameters
also has a Pareto Type II distribution, this time with parameters  and
and 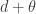 . The mean of a Pareto Type II distribution is always the ratio of the scale parameter to the shape parameter less one. Thus the mean of
. The mean of a Pareto Type II distribution is always the ratio of the scale parameter to the shape parameter less one. Thus the mean of 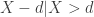 is as indicated in row 7 of the table.
is as indicated in row 7 of the table.
The limited loss  is defined as follows.
is defined as follows.
One interpretation is that it is the insurance payment when the insurance policy has an upper cap on benefit. If the loss is below the cap  , the insurance policy pays the loss in full. If the loss exceeds the cap
, the insurance policy pays the loss in full. If the loss exceeds the cap  , the policy only pays for the loss up to the limit
, the policy only pays for the loss up to the limit  . The expected insurance payment
. The expected insurance payment 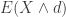 is said to be the limited expectation. For Pareto Type II, the first moment
is said to be the limited expectation. For Pareto Type II, the first moment 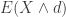 can be evaluated by the following integral.
can be evaluated by the following integral.
Integrating using a change of variable 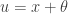 will yield the results in row 8a and row 8b in the table, i.e. the cases for
will yield the results in row 8a and row 8b in the table, i.e. the cases for 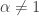 and
and  . A more interesting result is 8c, which is the
. A more interesting result is 8c, which is the  th moment of the variable
th moment of the variable  . The integral for this expectation can expressed using the incomplete beta function. The following evaluates the
. The integral for this expectation can expressed using the incomplete beta function. The following evaluates the ![E[(X \wedge d)^k]](https://s0.wp.com/latex.php?latex=E%5B%28X+%5Cwedge+d%29%5Ek%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Further transform the integral in the above calculation by the change of variable using  .
.
The integrand in the last integral is the probability density function of the beta distribution with parameters  and
and  . Thus
. Thus ![E[(X \wedge d)^k]](https://s0.wp.com/latex.php?latex=E%5B%28X+%5Cwedge+d%29%5Ek%5D&bg=ffffff&fg=333333&s=0&c=20201002) is as indicated in 8c.
is as indicated in 8c.
Now we consider two risk measures – value-at-risk (VaR) and tail-value-at-risk (TVaR). The value-at-risk at security level  for a random variable
for a random variable  is, denoted by
is, denoted by  , the
, the 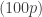 th percentile of
th percentile of  . Thus VaR is a fancy name for percentiles. Setting the Pareto Type II CDF equals to
. Thus VaR is a fancy name for percentiles. Setting the Pareto Type II CDF equals to  gives the VaR indicated in row 9 of the table. In other words, solving the following equation for
gives the VaR indicated in row 9 of the table. In other words, solving the following equation for  gives the
gives the 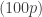 th percentile for Pareto Type II.
th percentile for Pareto Type II.
The tail-value-at-risk of a random variable  at the security level
at the security level  , denoted by
, denoted by 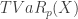 , is the expected value of
, is the expected value of  given that it exceeds
given that it exceeds  . Thus
. Thus ![TVaR_p(X)=E[X \lvert X>VaR_p(X)]](https://s0.wp.com/latex.php?latex=TVaR_p%28X%29%3DE%5BX+%5Clvert+X%3EVaR_p%28X%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Letting
. Letting 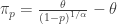 , the following integral gives the tail-value-at-risk for Pareto Type II. The integral is evaluated by the change of variable
, the following integral gives the tail-value-at-risk for Pareto Type II. The integral is evaluated by the change of variable 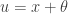 .
.
Tail Weight
Several properties in the above table show that the Pareto distribution (both types) is a heavy-tailed distribution. When a distribution significantly puts more probabilities on larger values, the distribution is said to be a heavy tailed distribution (or said to have a larger tail weight). There are four ways to look for indication that a distribution is heavy tailed.
- Existence of moments.
- Hazard rate function.
- Mean excess loss function.
- Speed of decay of the survival function to zero.
Tail weight is a relative concept – distribution A has a heavier tail than distribution B. The first three points are ways to tell heavy tails without a reference distribution. Point number 4 is comparative.
Existence of moments
For a given random variable  , the existence of all moments
, the existence of all moments 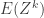 , for all positive integers
, for all positive integers  , indicates a light (right) tail for the distribution of
, indicates a light (right) tail for the distribution of  . The existence of positive moments exists only up to a certain value of a positive integer
. The existence of positive moments exists only up to a certain value of a positive integer  is an indication that the distribution has a heavy right tail.
is an indication that the distribution has a heavy right tail.
Note that the existence of the Pareto higher moments  is capped by the shape parameter
is capped by the shape parameter  (both Type I and Type II). Thus if
(both Type I and Type II). Thus if 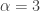 ,
,  only exists for
only exists for 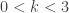 . In particular, the Pareto Type II mean
. In particular, the Pareto Type II mean 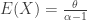 does not exist for
does not exist for 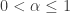 . If the Pareto distribution is to model a random loss, and if the mean is infinite (when
. If the Pareto distribution is to model a random loss, and if the mean is infinite (when  ), the risk is uninsurable! On the other hand, when
), the risk is uninsurable! On the other hand, when 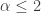 , the Pareto variance does not exist. This shows that for a heavy tailed distribution, the variance may not be a good measure of risk.
, the Pareto variance does not exist. This shows that for a heavy tailed distribution, the variance may not be a good measure of risk.
As compared with Pareto, the exponential distribution, the Gamma distribution, the Weibull distribution, and the lognormal distribution are considered to have light tails since all moments exist.
Hazard rate function
The hazard rate function 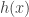 of a random variable
of a random variable  is defined as the ratio of the density function and the survival function.
is defined as the ratio of the density function and the survival function.
The hazard rate is called the force of mortality in a life contingency context and can be interpreted as the rate that a person aged  will die in the next instant. The hazard rate is called the failure rate in reliability theory and can be interpreted as the rate that a machine will fail at the next instant given that it has been functioning for
will die in the next instant. The hazard rate is called the failure rate in reliability theory and can be interpreted as the rate that a machine will fail at the next instant given that it has been functioning for  units of time. It follows that the hazard rate of Pareto Type I is
units of time. It follows that the hazard rate of Pareto Type I is 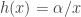 and is
and is  for Type II. They are both decreasing function of
for Type II. They are both decreasing function of  .
.
Another indication of heavy tail weight is that the distribution has a decreasing hazard rate function. Thus the Pareto distribution (both types) is considered to be a heavy distribution based on its decreasing hazard rate function.
One key characteristic of hazard rate function is that it can generate the survival function.
Thus if the hazard rate function is decreasing in  , then the survival function will decay more slowly to zero. To see this, let
, then the survival function will decay more slowly to zero. To see this, let 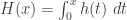 , which is called the cumulative hazard rate function. As indicated above, the survival function can be generated by
, which is called the cumulative hazard rate function. As indicated above, the survival function can be generated by 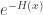 . If
. If 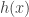 is decreasing in
is decreasing in  ,
, 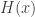 is smaller than
is smaller than 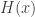 where
where 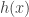 is constant in
is constant in  or increasing in
or increasing in  . Consequently
. Consequently 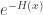 is decaying to zero much more slowly than
is decaying to zero much more slowly than 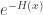 . Thus a decreasing hazard rate leads to a slower speed of decay to zero for the survival function (a point discussed below).
. Thus a decreasing hazard rate leads to a slower speed of decay to zero for the survival function (a point discussed below).
In contrast, the exponential distribution has a constant hazard rate function, making it a medium tailed distribution. As explained above, any distribution having an increasing hazard rate function is a light tailed distribution.
The mean excess loss function
Suppose that a property owner is exposed to a random loss  . The property owner buys an insurance policy with a deductible
. The property owner buys an insurance policy with a deductible  such that the insurer will pay a claim in the amount of
such that the insurer will pay a claim in the amount of  if a loss occurs with
if a loss occurs with  . The insuerer will pay nothing if the loss is below the deductible. Whenever a loss is above
. The insuerer will pay nothing if the loss is below the deductible. Whenever a loss is above  , what is the average claim the insurer will have to pay? This is one way to look at mean excess loss function, which represents the expected excess loss over a threshold conditional on the event that the threshold has been exceeded. Thus the mean excess loss function is
, what is the average claim the insurer will have to pay? This is one way to look at mean excess loss function, which represents the expected excess loss over a threshold conditional on the event that the threshold has been exceeded. Thus the mean excess loss function is 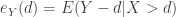 , a function of the deductible
, a function of the deductible  .
.
According to row 7 in the above table, the mean excess loss for Pareto Type I is  and for Type II is
and for Type II is 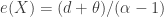 . They are both increasing functions of the deductible
. They are both increasing functions of the deductible  ! This means that the larger the deductible, the larger the expected claim if such a large loss occurs! If a random loss is modeled by such a distribution, it is a catastrophic risk situation.
! This means that the larger the deductible, the larger the expected claim if such a large loss occurs! If a random loss is modeled by such a distribution, it is a catastrophic risk situation.
In general, an increasing mean excess loss function is an indication of a heavy tailed distribution. On the other hand, a decreasing mean excess loss function indicates a light tailed distribution. The exponential distribution has a constant mean excess loss function and is considered a medium tailed distribution.
Speed of decay of the survival function to zero
The survival function 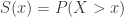 captures the probability of the tail of a distribution. If a distribution whose survival function decays slowly to zero (equivalently the cdf goes slowly to one), it is another indication that the distribution is heavy tailed. This point is touched on when discussing hazard rate function.
captures the probability of the tail of a distribution. If a distribution whose survival function decays slowly to zero (equivalently the cdf goes slowly to one), it is another indication that the distribution is heavy tailed. This point is touched on when discussing hazard rate function.
The following is a comparison of a Pareto Type II survival function and an exponential survival function. The Pareto survival function has parameters (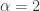 and
and 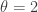 ). The two survival functions are set to have the same 75th percentile, which is
). The two survival functions are set to have the same 75th percentile, which is  . The following table is a comparison of the two survival functions.
. The following table is a comparison of the two survival functions.
Note that at the large values, the Pareto right tails retain much more probabilities. This is also confirmed by the ratio of the two survival functions, with the ratio approaching infinity. If a random loss is a heavy tailed phenomenon that is described by the above Pareto survival function (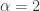 and
and 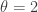 ), then the above exponential survival function is woefully inadequate as a model for this phenomenon even though it may be a good model for describing the loss up to the 75th percentile. It is the large right tail that is problematic (and catastrophic)!
), then the above exponential survival function is woefully inadequate as a model for this phenomenon even though it may be a good model for describing the loss up to the 75th percentile. It is the large right tail that is problematic (and catastrophic)!
Since the Pareto survival function and the exponential survival function have closed forms, We can also look at their ratio.
In the above ratio, the numerator has an exponential function with a positive quantity in the exponent, while the denominator has a polynomial in  . This ratio goes to infinity as
. This ratio goes to infinity as  .
.
In general, whenever the ratio of two survival functions diverges to infinity, it is an indication that the distribution in the numerator of the ratio has a heavier tail. When the ratio goes to infinity, the survival function in the numerator is said to decay slowly to zero as compared to the denominator.
The Pareto distribution has many economic applications. Since it is a heavy tailed distribution, it is a good candidate for modeling income above a theoretical value and the distribution of insurance claims above a threshold value.



 2017 – Dan Ma
2017 – Dan Ma
be a loss random variable. An insurance coverage with an ordinary deductible of
is purchased to cover the loss
. Of interest is the insurance payment per loss random variable
. The variable
is 0 if the loss
is below the deductible
and the variable
is
if the loss
exceeds the deductible
. The previous post demonstrates three approaches for calculating the variance of the payment per loss
.
in one of the three approaches:
as a mixture,
as a compound distribution.
is to be worked out in all three different methods.
2020 – Dan Ma
